Интерквартильный размах

Для того, чтобы посчитать интерквартильный размах выборки, нужно сначала найти ее медиану. Перед поиском медианы выборку следуют упорядочить. Если выборка содержит нечетное количество элементов, то центральный элемент и будет медианой. Если выборка содержит четное количество — медианой будет среднее арифметическое двух центральных элементов.

Разберемся, как найти интерквартильный размах для выборки с четным количеством элементов. Для начала ее нужно упорядочить от меньшего к большему:

Медианой в этой выборке будет среднее арифметическое двух центральных элементов:

После того, как найдена медиана всей выборки, ее нужно разделить на две части — левее медианы и правее, и найти медиану каждой половины:

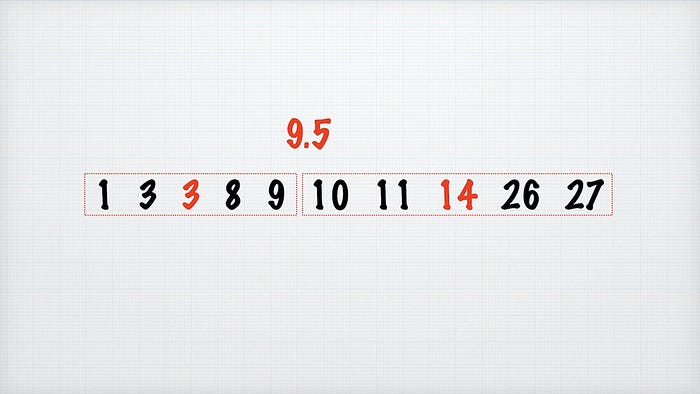
Медиана всей выборки — это второй квартиль, медианы левой и правой половин — это, соответственно первый (или нижний) и третий (или верхний) квартили:

Интерквартильный размах — это просто разность между третьим и первым квартилями:

В этом случае интерквартильный размах будет равен 14–3 = 11.

Для выборки с нечетным количеством элементов, размах считается практически так же. Разница состоит в том, что медиана выборки (или второй квартиль) — это центральный элемент, а первый и третий квартили считаются как среднее арифметическое двух центральных элементов подвыборок, лежащих слева и справа от медианы всей выборки (не включая саму медиану):

В этом случае интерквартильный размах будет равен 20–3 = 17.

Кстати, первый, второй и третий квартиль еще называются, соответственно, 25-й, 50-й и 75-й перцентиль. Поэтому, когда вам говорят, что уровень зарплаты для вашего грейда считается как 75-й перцентиль от уровня зарплат по рынку, имеют ввиду именно третий квартиль.